算数〈中学受験〉『相似比1:2の円すいの体積比1:8』を視覚で確かめたい！

相似比が1：2の円すいの体積に関する問題が出てきた時にふと気になったこと。
体積比が1：8になるのは、理論的には納得できるけど、立体を想像してみると…
「ホントに1：8！？」
「イメージでは1：5くらい…」そう思い、「ならば実際に立体で体感してみよう！！」とウチのコと展開図を組み立て体積を見比べてみることに。

数の大きさだったり、長さ、重さ、大きさを、理屈だけではなく感覚的にもつかめていることは、算数の問題を解く上でとっても有利。ちょっと休憩がてら、模型を組み立てて視覚でボリューム感を確認してみるのはいかがでしょうか？
使用した展開図も載せていますので、同じように『１：８』が信じられない人、工作好きの人は良かったら作ってみてください！

体積比を式から確認

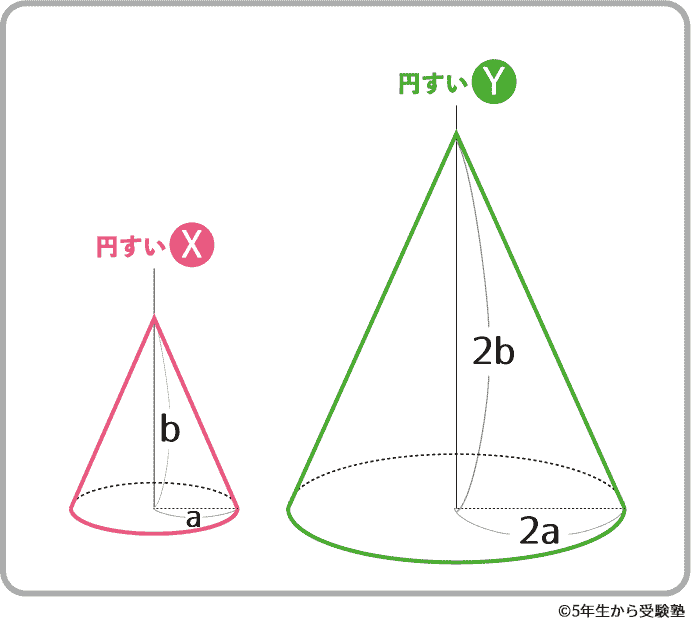
まずは念の為、体積比を式で確認！
上のような相似比が『１:２』の二つの円すいのそれぞれの体積は…

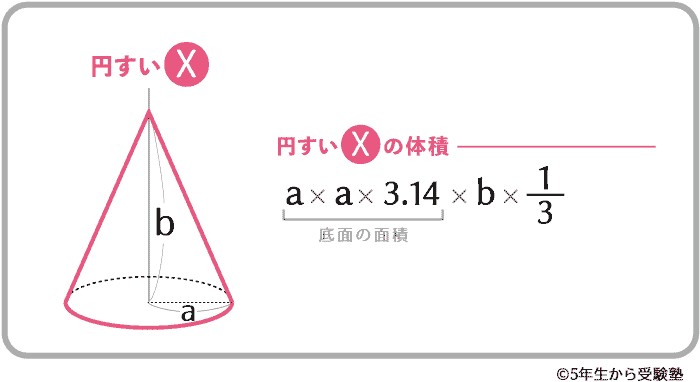
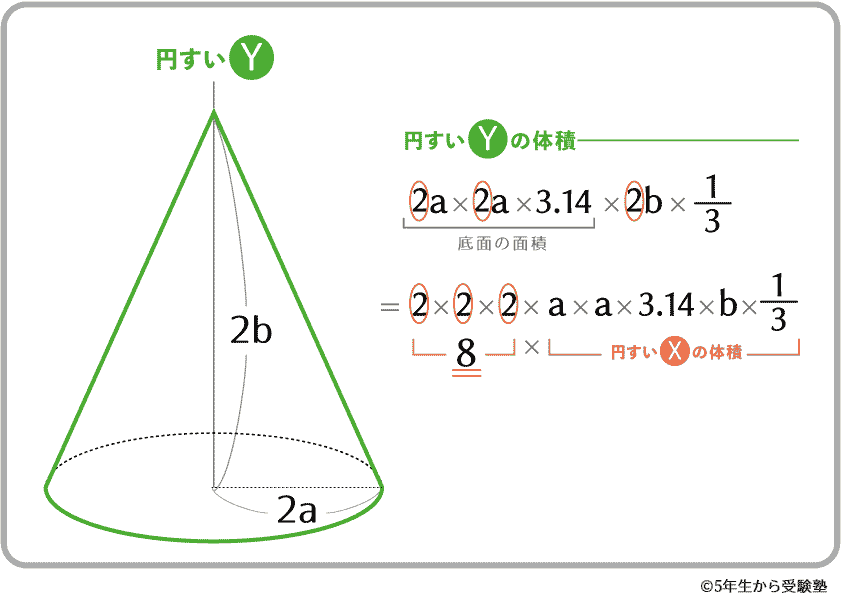
上のようになり、体積比は

円すいX : 円すいY = １：８

ということが、式から確認できます。

立体模型を作成

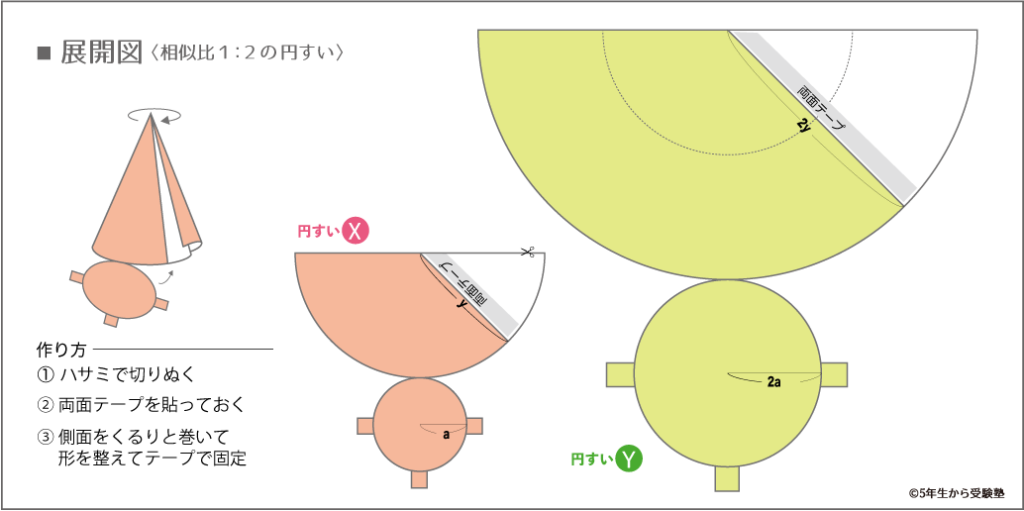
相似比『１：２』のピンクの円すいと緑の円すいの立体を組み立てます。
下のさらっとおさらい資料からA4データをダウンロードできます。
厚紙にプリントして作ってみてくださいね。

■作り方
①展開図を切り抜く
②のり白部分に両面テープを貼っておく
③紙をくるりと巻き、形を整えて両面テープで固定

立体模型から確認

早速、相似比『１：２』の円すいを見比べてみました。

緑の円すいの底面の半径、高さは（母線も）ピンクの円すいのそれぞれの長さの2倍になっています。
緑の円すいの点線より上の部分が、ピンクの円すいと同じ大きさの部分。

つまり、緑の円すいの点線より下の部分はピンクの円すいの体積の『7倍』。

ピンクの円すいを緑の円すいにかぶせてみると（点線より少し浮いてしまっていますが）こんな感じ…

ウチのコも、「そんなにあるかな？？」という感じでイマイチピンと来てない様子。
想像したよりは、緑の円すいにボリュームの大きさは感じますが…


こうして実際に立体を見て分かったこと、それは…

円すいの体積は感覚でつかむのが難しい！

ということ…

それでも、こんなふうに実際に立体に触っていると
『円すいって、下の方にこんなにボリュームがあるんだ』ということは実感できました。

まとめ

今回は、『相似比が１：２の円すいの体積比は1：8』を実際に立体を作り視覚で確かめてみました。

結論としては、
・視覚で見ても『１：８』には感じない！
・円すいの体積は実際に見ても把握しにくい

ということに。

ただ、一度見た目で確認したことは、今後算数の問題を解く上で活きてくる、と思うのです…

ウチのコも実際に立体に触れて、「こんな感じになるんだー」と、やはりイメージとは違った様子。
今後、円すいの問題を問題用紙の上だけで理解するより、グッと身近に感じるられるようになったはず！

算数の問題は、難しくなるほど抵抗感が生まれてしまいがち。『身近なところにある事象の延長上の問題』として捉えて、リラックスして解いて欲しいと思います。

ただ、学年が上がるにつれ、こんなふうに工作をして確かめている時間は無くなっていくもの…
なので、余裕のある低学年・中学年のうちに、このように遊びながら学ぶ知育というものが大事なのかも、と改めて気づきました。

これから、本格的に受験勉強を始める！という方は、ぜひこんな学び方も取り入れてみてください。


にほんブログ村